Детские задачи

В статье рассматривается важность детских задач для развития у детей логического мышления, креативности и аналитических способностей. Описываются различные виды детских задач, такие как головоломки, логические задачи и задачки на развитие математических способностей. Также обсуждаются психологические аспекты задач и как они помогают в развитии самостоятельности и уверенности в своих силах. В заключение статьи предлагаются полезные рекомендации для родителей и педагогов по использованию детских задач в обучении и развитии детей.

1. Некто купил 96 яблок, платя за каждые три яблока по гривеннику, а затем еще 96 яблок, платя за каждые два по гривеннику; все эти яблоки он продал, получая за каждые пять яблок по двугривенному. Получил ли он барыш или потерпел убыток?

2. Виноторговец имел квадратный подвал, вокруг которого, вдоль всех четырех стен, было сделано восемь отделений для бочек с вином, так что вдоль каждой стены приходилось по три отделения, два угловых и одно среднее. Купив 32 бочки, он приказал своему приказчику расставить эти бочки по отделениям так, чтобы вдоль каждой стены подвала стояло по девяти бочек. Приказчик исполнил это так: поставил по одной бочке в угловые отделения и по семи в средние.

В продолжение недели приказчик украл четыре бочки, но переставил остальные так, что при поверке торговец нашел вдоль каждой стены по девяти бочек. И так приказчик крал три раза, каждый раз по четыре бочки, а остальные переставлял так, что купец при поверках всегда находил вдоль каждой стены по девяти бочек. Спрашивается, в каком порядке стояли бочки после первой, второй и третьей покражи?

3. Человек нес капусту и вел волка и козу. Подошед к реке, он увидел такой маленький челнок, что сразу посадить в него фиг двоих, кроме себя, не решился. Как он перевез порознь капусту, козу и волка на другую сторону реки, не дав козе случая съесть капусту, а волку — козу.

4. На изображении 1 обозначены четыре дома b и четыре дома а; посредине же находится колодец, который принадлежит жителям домов b. Надобно построить такой забор, чтобы жители из домов а не могли подойти к колодцу, а жители домов b имели бы к нему свободный доступ. Как построить такой забор?

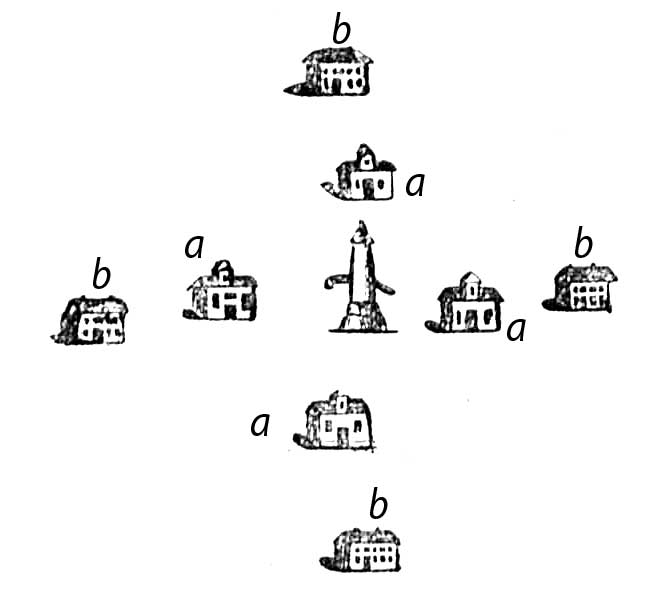Изображение к задаче 4 Изображение 1

5. На шестнадцати бумажках напишите: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 и 16. Затем попытайтесь разложить их по четыре в ряд в четыре ряда так, чтобы сумма по прямым линиям была в каждом ряду 34.

6. Подобно предыдущей задаче, напишите на бумажке числа до 9 включительно и расположите их по три в ряд в три ряда так, чтобы сумма цифр не только по горизонтальным и вертикальным линиям была 15, но и по диагоналям.

7. Наконец, решите еще более сложную задачу. Напишите числа до 100 включительно и расположите их по 10 в ряд в 10 рядов так, чтобы сумма чисел, как в горизонтальных рядах, так и в вертикальных и по диагоналям, была 505.

8. Одному человеку очень понравилась у барышника лошадь, и, спросив ее цену, он узнал, что барышник желает получить: за первый гвоздь в подкове лошади одну копейку, за второй - две, за третий - четыре, за четвертый - восемь и т. д. , удваивая ценность каждого гвоздя во всех четырех подковах. Что стоила лошадь, если каждая подкова прибивается шестью гвоздями?

9. От девятнадцати отнимите единицу так, чтобы получилось двадцать.

10. В Англии был построен громадный пароход Грет-истерн, который рассчитан на перевозку 1.350.000 пудов груза. Если-б вы посещали этот пароход раз в каждую неделю, и в первое свое посещение уронили бы одну булавку, во второе - две, в третье - четыре и т. д., при каждом посещении удваивая число оброненных булавок, то по прошествии года, 52 недель, пароход давно должен был бы утонуть, так как он не в состоянии был бы выдержать оброненных вами 4.503.599.627.370.495 булавок, которые весили бы около 37.697.541.480 пудов.

11. Говоря о громадных числах, подумали ли вы когда-нибудь о том, что такое биллион? Вы знаете, что это миллион миллионов, но, тем не менее, чтобы понять всю громадность этого числа, посмотрим, сколько времени надобно употребить, чтобы сосчитать до биллиона. В одну минуту вы можете сосчитать до 160 или 170; допустим, что вы считаете очень быстро и можете сосчитать в минуту до 200, что составит в один час 12.000; в сутки - 288.000; в год или 365 дней (чрез каждые четыре года, в високосные года, вы можете денек отдохнуть) - 105.120.000. Предположим, что Адам с самого начала своего существования начал считать и продолжал бы считать до нашего времени, то и он не досчитал бы до биллиона, так как для этого потребовалось бы 9.512 лет, 34 дня, 5 часов и 20 минут безостановочного быстрого счета.

12. Число 45 можно разделить на четыре части так, что, отняв от первой части 2 и прибавив их ко второй части и помножив третью часть на 2 и разделив четвертую часть на 2, все части составят 40.

Первая часть 12 без двух 10

Вторая             8 да два     10

Третья             5 на два     10

Четвертая     20 на два     10

                      45                 40

13. Продавец купил 120 яблок по две штуки за копейку и затем еще 120 яблок, платя за три штуки копейку. Смешав все яблоки, желая только выручить свои деньги, он стал так и продавать каждые пять штук за две копейки. Был ли верен его расчет?

За первые 120 яблок он заплатил 60 к., да за вторые 40 к., итого -1 р. Выручил же за 240 яблок, т.-е. за 48 пятков по 2 к. - 96 к. Следовательно, потерпел убытку 4 к.

14. У вас 13 товарищей, которым вы хотите раздать 12 яблок. Одному придется остаться без яблока; вы решили, которого следует лишить яблока, но не знаете, как бы сделать, чтобы ему было необидно.

Поставьте всех в кружок и скажите, что вы предоставляете случаю решить, кому остаться без яблока. Начав с третьего человека, стоящего по левую руку от того, которому вы не желаете дать яблока, вы считаете до девяти; девятому вручаете яблоко и просите выйти из круга. Продолжая так считать, вы раздаете все ваши двенадцать яблок, а один, которому вы не намеревались дать яблока, его не получит.

15. Составьте из цифр 1, 2, 3, 4, 5, 6, 7, 8 и 9 такие числа, чтобы чрез сложение получить ровно 100.

16. Какие четыре гири должно сделать, чтобы быть в состоянии этими четырьмя гирями взвешивать всякое число фунтов, от одного до сорока.

17. Если-б вам предложили соломинкою поднять бутылку, то таким предложением, я думаю, озадачили бы вас немало, а между тем, сделать это далеко не трудно. Выбрав цельную, немятую соломинку, возьмите бутылочку, надломите соломинку, просуньте ее углом в бутылку так, чтобы короткий конец уперся внутри в бутылку, и вы будете в состоянии поднять бутылку, держа только за длинный конец соломинки.

18. Число 73 имеет странную особенность: если вы станете умножать его на три и последовательно на все множители трех, то получите:

73 X 3 = 219

73 X 6 = 438

73 X 9 = 657

73 X 12 = 876

73 X 15 = 1095

73 X 18 = 1314

73 X 21 = 1533

73 X 24 = 1752

73 X 27 = 1971

Рассматривая все произведения в том порядке, как они получились, мы видим, что в единицах соблюден такой порядок: 9, 8, 7, 6, 5, 4, 3, 2 и 1. Рассматривая же одновременно десятки и сотни, мы получим обратно: 1, 2, 3, 4, 5, 6, 7, 8, 9 и даже 10.

19. Вы можете очень просто отгадать число очков на двух косточках, не смотря на них.

Попросите кинувшего косточки удвоить число очков одной из косточек, прибавить к этому 5, сумму эту помножить на 5 и к полученному произведению прибавить число очков другой косточки.

Узнав результат такого исчисления, вычтите из него 25, и тогда в полученном числе вы будете иметь две цифры, из которых одна будет означать число очков на одной косточке, а другая - на другой.

Предположим, что выкинуто 2 и 3; удвоив 2, получим 4, прибавив 5 = 9, помножив 9 на 5 = 45, прибавим 3, число очков другой косточки, получим 45 + 3 = 48, и, наконец, вычтем из 48 - 25 = 23. В этом числе две цифры 2 и 3, которые показывают число очков на косточках.

20. Некто имел квадратный фруктовый сад, с десятью деревьями, с домом между ними, как видно на изображении 2, и захотел этот сад разделить между своими пятью сыновьям так, чтобы все получили совершенно одинаковые равные части земли и чтобы у каждого было по два дерева. Как разделить ему свой сад?

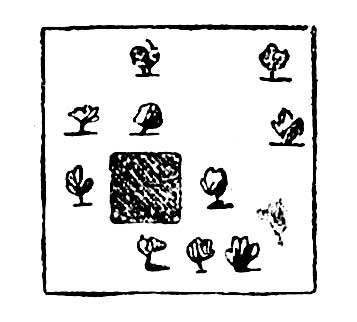
Изображение к задаче 20
Изображение 2

21. Вырежьте из тонкой дощечки сердце и сделайте в этой дощечке шесть небольших отверстий, как показано на изображении 3.

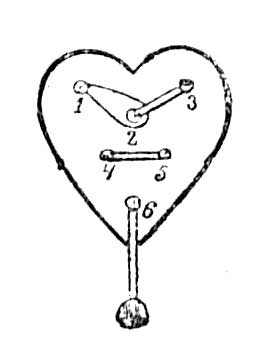
Изображение к задаче 21

Изображение 3

Взяв тонкий шелковый шнурок раз в восемь длиннее сердца, сложите его два конца и врежьте их в деревянный шарик. Петлю этого шнурка проденьте через отверстие 6 с лицевой стороны, чрез 2 с левой стороны, затем чрез 3, 5, 4, 1 и, наконец, с лицевой стороны опять чрез 2, с левой стороны чрез 6 и чрез петлю пропустите шарик; затем остается только протянуть петлю обратно чрез 6-е и 2-е отверстия. Не многие из ваших товарищей догадаются, как снять шнурок, не разрезывая его.

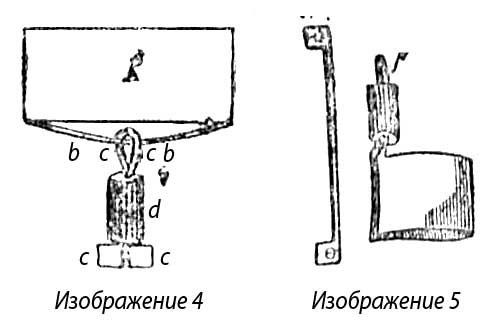
22. Вот еще задача подобного же рода. На изображении 4 А изображает игральную карту, от которой отрезана узкая полоска bb, но отрезана не совсем, а так, что концы этой полоски остаются неотделенными от карты, d - кусок трубки, который висит на полоске карты сc, удерживаемый широкими четыреугольными концами ее. Задача состоит в том, чтобы снять трубку, ничего не испортив. Ясно, что трубка была надета на полоску карты, а следовательно, и может быть снята. Изображение 4 покажет нам, как надеть трубку, а, следовательно, и как снять. Слегка, так, чтобы не сломать карты, согните карту А пополам; тогда полоска bb также согнется и отделится книзу; эту полоску проденьте чрез трубку так, чтобы она петлею f вышла из другого конца трубки. Чрез петлю f проденьте полоску ее до половины, затем остается только вдвинуть обратно в трубку петлю f вместе с согнутою полоскою ее, выпрямить карту А, и получим то, что представлено на изображении 5.

Изображение к задаче 22

23. Из трех ножей и трех рюмок можно составить довольно прочный мостик. Поставьте три рюмки треугольником в равном друг от друга расстоянии (на длину столового ножа). На рюмки положите три ножа так, чтобы ножи были положены на рюмки все своими ручками; нож 1 опирается на 2, а 2 - на 3, который, в свою очередь, опирается на нож 1 (изображение 6).

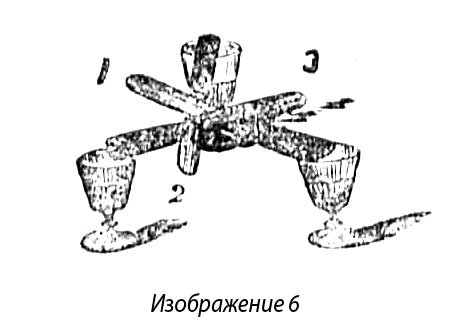
Изображение к задаче 23

Если переплетете так ножи, то получите мостик, который может выдержать довольно большую тяжесть.

24. Если вы закупорите бутылку пробкою, воткнете в эту пробку булавку и попробуете на головке этой булавки уставить другую пробку, то найдете, что сделать это не легко. Если же вы в эту вторую пробку воткнете с двух сторон по вилке, то пробка будет не только прочно стоять на головке булавки, но ее можно будет раскачивать, и то она не упадет.

25. Многие умеют поддерживать равновесие палки, поставленной на конец пальца, и действительно, сделать это не трудно; нужно только внимательно следить за верхним концом палки и при наклоне палки подвинуть и палец в ту же сторону, тогда палка примет опять вертикальное положение. На ноге балансировать палку уже гораздо труднее, потому что нога нас не так хорошо, слушается, как рука. На голове же еще труднее удержать палку в равновесии, так как здесь вы не видите ее наклона, а можете только чувствовать его, но если будете практиковаться, то можете достигнуть даже возможности балансировать палку не только на голове, но одновременно и на ноге.

26. Чтобы поставить куриное яйцо на носок, не надламывая скорлупы, достаточно взболтать яйцо настолько, чтобы желток смешался с белком, и затем подержать несколько минут яйцо носком книзу. Желток, будучи значительно тяжелее белка, осядет книзу и даст вам возможность довольно легко поставить ваше яйцо на носок.

 

Список используемой литературы:

  • И.Я. Герд - Игры для детей всех возрастов (7 изд.) - Ленинград, 1926 - С. 208

Возможно вам будут интересны другие игры для детей

Главная » Детские игры » Задачи
Связь